Supply Chain Modelling for a Resource Allocation Model Using Spreadsheets

This example aims to present the classical resource allocation model for two products by discussing this from a supply chain perspective.

The model developed here uses spreadsheets in MS Excel and Solver. A set of performance measures are considered and analyzed.

This model is part of the material presented in Chapter 7 in the book Supply Chain Analytics and Modelling by Nicoleta Tipi © 2021.

Characteristics of linear programming models

Models using the linear programming technique have the following characteristics:

Variables

The elements that we try to identify within a linear programming model are known as variables. These could be number of products to produce, or number of products to transport, or number of workers required per shift and so on.

Defining the variables is a key step in solving linear programming models and they form part of the mathematical model. 

Constraints

The set limitations within the objective function of a model that can be reached are known as constraints. 

It is particularly important to include the full list of constraints when aiming to solve a linear programming model. However, some of these may not be incorporated if they do not significantly affect the final outcome.

There are non-negativity constraints, where the variables we look to identify are >= 0.

Constrains could also consider integer constraints, where the variables are expected to be ‘full’ values. For example, in solving a linear programming model that aims to produce a chair, the integer constraint will ensure that no partial chairs are being produced. There are also constraints that will be identified as inequality constraints.

Objective function

These models are characterized by having an objective function. In general, this is set to maximize, for example, ‘profit’ or minimize, for example, ‘cost’. This function needs to be clearly defined as a mathematical function.

When only one objective function is defined, the model is known as a single objective function model. However, having only one objective function model doesn’t imply that the model only deals with one performance measure. Within a single objective function, more than one performance measure could be set to characterize the model (such as cost, deliver in full, resource utilization, available inventory and others).

There are also mathematical models that operate with multiple objective functions, where more than one objective is developed and optimized mathematically.

Resource allocation model

Resource allocation models aim to maximize their objective by meeting resource constraints.

For this type of model, the resources are divided and assigned to competing activities (Baker, 2016; Powell and Baker, 2011).

This model has the potential to consider more than one dimension within a supply chain. It can incorporate details about the manufacturing process, the volume, the number of products to be produced, the quantity of raw materials or semi-finished products supplied, and could also incorporate details about customer demand.

However, although the model works only with one optimization function (maximize profit), more than one performance measure can be observed in this context, such as: maximum profit, throughput, resource availability and resource utilization and customer service.

To understand this type of model in the context of supply chain, the following example is presented, analyzed and discussed: the resource allocation for two products.

This example is mainly analyzed from a manufacturing point of view, where information and data are available to and from the suppliers and customers.

Resource allocation example

A manufacturing organization aims to bring further understanding to its operations with specific reference to two of its key products (namely NT111 and NT112).

The company has identified a set of issues with these two products and aims to gain further understanding from analysing these using prescriptive analytics.

Identified issues

There are issues concerning the available time allocated for producing these two products in the manufacturing and assembly department.

There are issues identified with raw materials available in stock from two suppliers.

Many other issues can be considered for analysis at this stage, but the two main aspects that are of concern are those presented above. The analysis is intended from the point of view of the total profit generated by producing these two products, considering the issues identified above.

By producing these two products, the company is able to provide an estimate of the profit per product as well as an overall profit.

Before the analysis can start, the first point for consideration is regarding data. In general, this is data that is available internally within the organiza¬tion’s IT system, or needs to be collected by an analysis of internal sources.

Input data

To start the analysis the following input data is required:

• Raw material required per product. This type of data is a product design characteristic and is indicated at the product design stage, and it will be present in the bill of materials that forms this product. It is important to realize that this is a detail that is not changeable. As soon as changes are to be considered to this component, the overall product characteristics change. Therefore, changes in product design and changes in the characteristics of its components will result in a new product.
  
  
• Total number of units sourced from suppliers. This type of data is available from the sourcing/buying department. This is a value that can change for a number of reasons, some of which may be: the stock availability at the supplier end, or at the manufacturer end, the delivery conditions and the quality of the raw material supplied.
  As this information is linked to stock availability, inventory control managers also deal with this type of information.
  
  
• Time required to produce the indicated products. This type of information is part of the product characteristics, identified through the design process that can, for example, clearly specify the time required for a product to be processed at a particular machine. This type of data is unchangeable and will be captured in the bill of materials for each product.
  This is relevant to the planners, manufacturers and operations managers. However, there may be an added component to this; waiting time in the queue to be processed that potentially can be reduced with a more optimal operation. This will be a dynamic component, and however relevant it is to consider this aspect, for the purpose of this example it will not be taken into consideration. Only a static component is considered.
  
  
• Total time allocated for producing these two products. This information is provided by the production planner, and depends on the resources available in the manufacturing departments. This value can change due to staff and/or machine availability. However, other issues could be encountered at this point when unpredictable disturbances occur, for example, with machine downtime, accidents or power cuts.
  
  
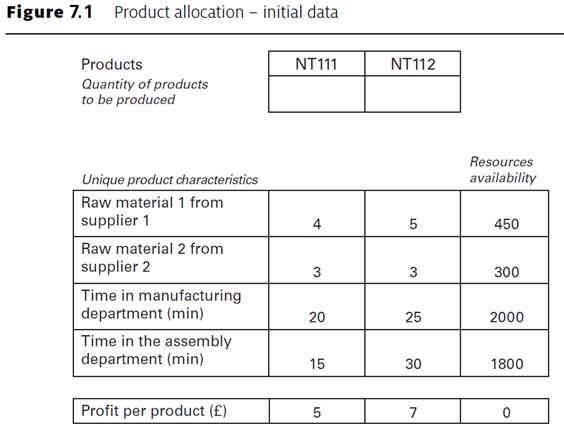
• Profit per product. This detail is available from the finance department within an organization and is in general based on past information as well as details acquired from current market conditions. These details may be readily available within the ERP system; however, time may be allocated to allow for the collection of this information. These details are presented in Figure 7.1.

• Scope. The scope of the analysis is threefold:
  
  
  • Identify the total number of products to be produced.
  • Maximize the profit to produce these two products.
  • Maximize the use of the resources put in place for producing these products.
    
    
• Output data. The output data obtained at the end of the analysis is as follows:
  
  
  • Quantity to be produced per product.
  • Quantity of raw material used in production.
  • Leftover inventory of raw materials supplied.
  • Overall time spent in production per department.
  • Resource utilization.
  • Total profit. 

Therefore, in this particular example, we are dealing with fixed and variable data as well as data this is required from different locations and functions within a company.

The performance measures that can be identified within this model are as presented in Table 7.1.

As soon as the data collection process has been completed, the analysis can continue by employing a linear programming optimization approach.

To work with a linear programming approach, three elements are to be defined: the variables, the constraints and the objective function by which we aim to evaluate a situation. This will form the mathematical model as detailed below.

Variables

Following these particular examples, the variables are the total number of products to be manufactured, therefore the total number of NT111 and NT112.

We may want to represent these using mathematical notations such as X and Y; however, for this example, we will avoid using these notations. 

• Variable 1: Total number of products to be NT111.
• Variable 2: Total number of products to be NT112.

Constraints

In this particular case, there is a set of limitations that need to be considered. These are supplier-related constraints named raw material 1 and raw material 2. There are also manufacturing dependant constraints named manufacturing time and assembly time:

• Raw material 1: The total quantity of raw material 1 required to produce the two products is less than or equal to the quantity available in stock for raw material 1.
  
  
• Raw material 2: The total quantity of raw material 2 required to produce the two products is less than or equal to the quantity available in stock for raw material 2.
  
  
• Manufacturing time: The total time required in the manufacturing department to produce the two products is less than or equal to the total allocated time.
  
  
• Assembly time: The total time required in the assembly department to produce the two products is less than or equal to the total allocated time. 

To work with the linear programming representation, two other types of constraints are to be considered. First is the non-negative constraint that refers to the set of the two variables to higher than or equal to value '0'. This implies that we should not expect negative values as part of the solution. 

Variable 1; Variable 2 >= 0

There is also the expectation that we will have 'integer' values. In other words, we will expect to work with full products.

Variable 1; Variable 2 = interger

Objective function

To complete the setting of our linear programming model, the objective function is required. In this case, we will have as an objective the total profit that we will want to maximize.

Total profit = maximize (total profit)

The mathematical model is now set. This model can be implemented and solved in Excel using the add-in software Solver. Considering the data set as presented in Figure 7.1, based on the input data collected a template can be developed in Excel that captures all the required elements, as shown in Figure 7.2.

Solving this example in Excel, the following formulas need to be considered for each of the constraints set.

In cell F5 input =SUMPRODUCT(D5:E5,$D$2:$E$2)

In cell F6 input =SUMPRODUCT(D6:E6,$D$2:$E$2)

In cell F7 input =SUMPRODUCT(D7:E7,$D$2:$E$2)

In cell F8 input =SUMPRODUCT(D8:E8,$D$2:$E$2)

The value for the objective function to maximum profit will be listed in H10. This will have the formula =SUMPRODUCT(D10:E10,D2:E2)

Using Solver

Having set up all the forumlas in the template, the model is now ready to be solved using Solver. Solver is an add-on programme that will need to be set up in Excel:

In Excel, select File > Options > Add-ins > Solver Add-in and select "Go". 

The Solver will appear under the Data tab in Excel. As presented in Figure 7.3, individual settings for the variables, constraints and the objective function can be set. 

Variables

Variable 1 is under cell D2 and Variable 2 is under cell E2. Therefore, in Solver, these will inputted in the section "By Changing Variable" cell as $D$2:$E$2.

Constraints

The raw materials and time to produce constraints in this case, are in cells F5, F6, F7 and F8. In Solver you need to press "Add" to open then add constraints values, as indicated in Figure 7.4.

For the non-negative constraints, the following condition needs to be ticked: "Mark Unconstrained Variables Non-Negative".

Within the option "Select a Solving Method" use "Simples LP" (see Figure 7.3). 

Setting up the variables as integer numbers, the following is to be considered: $D$2:$E$2 = integer.

The objective function

In Solver in the "Set Objective", select $H$10 and then select "Max" (Figure 7.3). This will maximize the function inserted in cell H10. At this point the model will be ready to run Solver by selecting "Solve".

The results are obtained as presented in Figure 7.5.

The data obtained as a result of solving this model is Quantity to be produced per product. It can be noted that the results for each product are listed in cells D2 and E2 respectively.

Quantity to be produced for product NT111 = 66 units, and Quantity to be produced for product NT112 - 27 units. Therefore, the total quantity to be produced is 93 units in total.

• Quantity of raw material used in production. The results in this case are listed under the cells F5 and F6. It can be noted that the quantity used in production is less than the quantity available in stock.
  
  
• Overall time spent in production per department. The results are listed under the cells F7 and F8. It can be noted that the time spent is less than or equal to the time available, and at this point there is some time left (5 min, see cell I7) in the manufacturing department, but not in the assembly department.
  
  
• Total profit. The total profit is listed in cell H10 with a value of £519. 

A response to the set of performance measure for this model can now be noted in Table 7.2.

To make best use of this model for decision-making, a number of 'What if...?' scenarios could be considered for the analysis. These scenarios may include:

1. What if the stock available for both raw materials increases? Let's assume as an example that the values will be double from the original setting. Without any change in the time allocated for producing these products, it can be noted that there will be no changes in the results obtained after running Solver again.
   
   
2. What if the demand for product 2 is set to 40 units? This change can be inserted as one of the constraints in the system, however it will produce results as indicated in Figure 7.6. In this case, it can be observed that the production is better balanced, but there are more materials left in stock as well as more time unsued in the manufacturing department. The profit in this case is now lower, too. 

Conclusion

In conclusion, it can be noted that although this tool is mainly used for optimization, it can also be used for prediction.

Setting up a model will allow understanding on a number of performances, as indicated in Table 7.2.

A number of other scenarios can be considered in the case of this model, such as different demand per product, where the performance measure will be to meet the customer demand, not necessarily to maximize throughput, or maximize profit. Similar examples are detailed in publications such as Baker (2016, p 29) with an example on Brown Furniture Company discussing the allocation of three products.

There is the opportunity for this type of model to be used for prediction and to further enhance the decision-making process for managers in the supply chain.

References

Baker, K R (2016) Optimizaition Modelling with Spreadsheets, 3rd edn, Wiley, Hoboken, NJ

Powell, D G and Baker, K R (2011) Management Science: The art of modeling with spreadsheets, 3rd edn, John Wiley & Sons, Hoboken, NJ

Tipi, Nicoleta (2021) Supply Chain Analytics and Modelling: Quantitative Tools and Applications, Kogan Page, UK